Quick, what’s the first image that comes to mind when you see the word “mathematics?” For most of us, it’s probably a bunch of calculations – perhaps droves of numbers being added or multiplied. Do a Google image search, and you’ll see more calculations – scribbled on blackboards, spilling out of notebooks. But math is really more about ideas than calculation, a fact so under-recognized that I’ve just written a book, The Big Bang of Numbers, to make this point.
Take something as basic as multiplication. Many might still remember it appearing mysteriously right after addition, with the exhausting requirement of having to memorize their “times” tables. But what is multiplication? What’s its underlying idea? The answer (explained much better in some schools now, compared to when I was a child) is that it’s simply addition in disguise! You abbreviate “ten times” as “6 times 10” and instead of laboriously performing all those additions, come up with the answer instantly from your “six times” table.
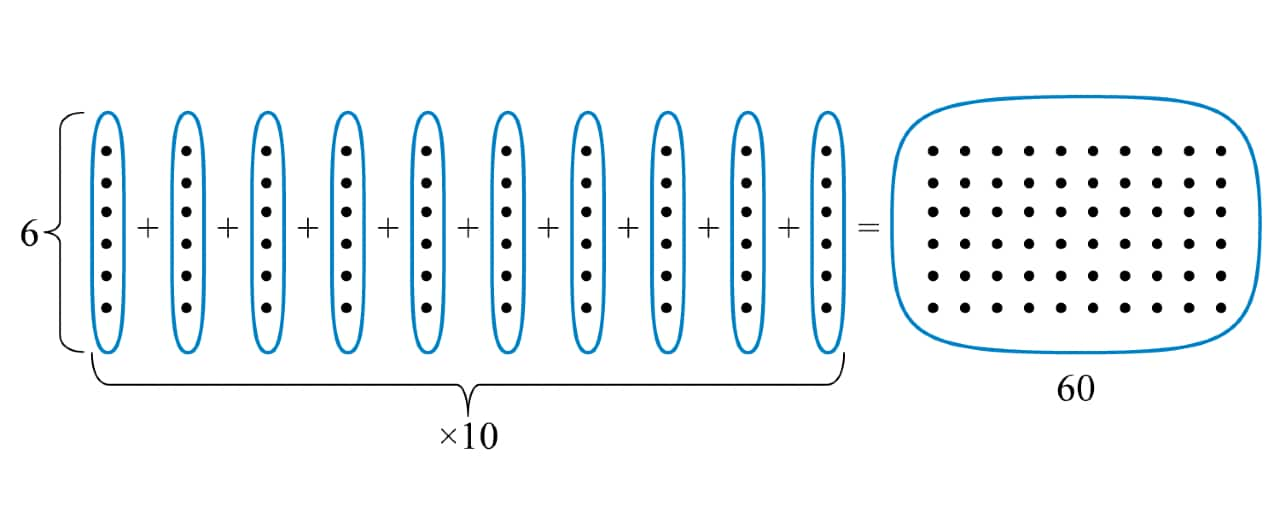
So multiplication is a zippy way to add, is what you want to tell kids. Try having a contest where you use addition and they use multiplication to find the same answer, and see how their victory over you motivates them to master their tables!
You can do a similar deep-dive through other clouds of calculation to try and find the basic idea mathematics is trying to express. For instance, subtraction simply arises from the need to have some way of undoing addition. Add 2 to 1 to get 3, subtract 2 from 3 to get back 1. But then you encounter a problem. Try subtracting 3 from 2 instead, and you’re stuck, since no positive whole number corresponds to the answer. That’s when you realize you need to create new numbers, the negatives. Note how much easier this makes it to accept negative numbers, which for centuries were labelled “false” and “nonsense” even by famous mathematicians like Descartes and Pascal.
There’s something else the above two elementary examples help illustrate: many of the ideas in mathematics involve recognizing patterns. For instance, once you see the schematic for 6x10, you can create similar ones for 7x10, 6x11, and so on. Also, once you define subtraction as a means to undo addition, you can similarly define division as a way to reverse multiplication. This leads to an analogous problem – the need to find new numbers that can handle divisions like 1 divided by 2 or 2 divided by 3. Following the pattern with which you handled subtraction leads you now to create the fractions.
Patterns, of course, abound everywhere – from the giant spirals formed by faraway galaxies, to the branching distribution of air vessels in our lungs, to the exponential way viral epidemics initially evolve. It is no wonder then that mathematics, which is often called the study of patterns, is so good at describing our universe. The point I make in my book is that we can be bad at performing computations, but still understand and enjoy these descriptions offered by maths, since these take the form of ideas, not calculation.
However, if one wants to practically apply mathematics to make predictions or solve problems, rather than just appreciate the subject, then one has to calculate. That’s why it’s not enough to just understand the idea behind multiplication – we need to remember our tables well enough to recall answers instantly when needed. Such basic numerical fluency has been shown to increase our ability to solve harder problems.
To further illustrate these different aspects of maths, let’s see how ]they play out in the stock market. The million-dollar (or rather 120.4 trillion dollar, the 2021 value of the global stock market) question is whether there are patterns in the way share prices work.
Several websites on the internet say yes. Certainly, if one analyzes multitudes of historical records, one can isolate short bursts where the price curve behaves like an “ascending triangle” or “double bottom” or all the other colorfully named recurring patterns that have been identified. Unfortunately, even if you believe you are in one of these patterns, there is no guarantee that it will continue – the price could quickly transition to some other pattern, or even suddenly crash.
One way to improve this picture is to allow the possibility of sudden price swings in the modelling. Such analysis starts with the assumption that there is some amount of self-similarity in market behaviour, i.e. that in a statistical sense, the price shows the same types of ups and downs over the course of a day that it might over the course of a month or year (though at increasingly magnified scales). Indeed, look at a typical stock price, and you will see that the larger swings resemble the zigzag profile of the smaller swings. Such self-similar curves are (roughly) called fractals, and their incorporation can lead to better mathematical models for the behaviour of the stock market.
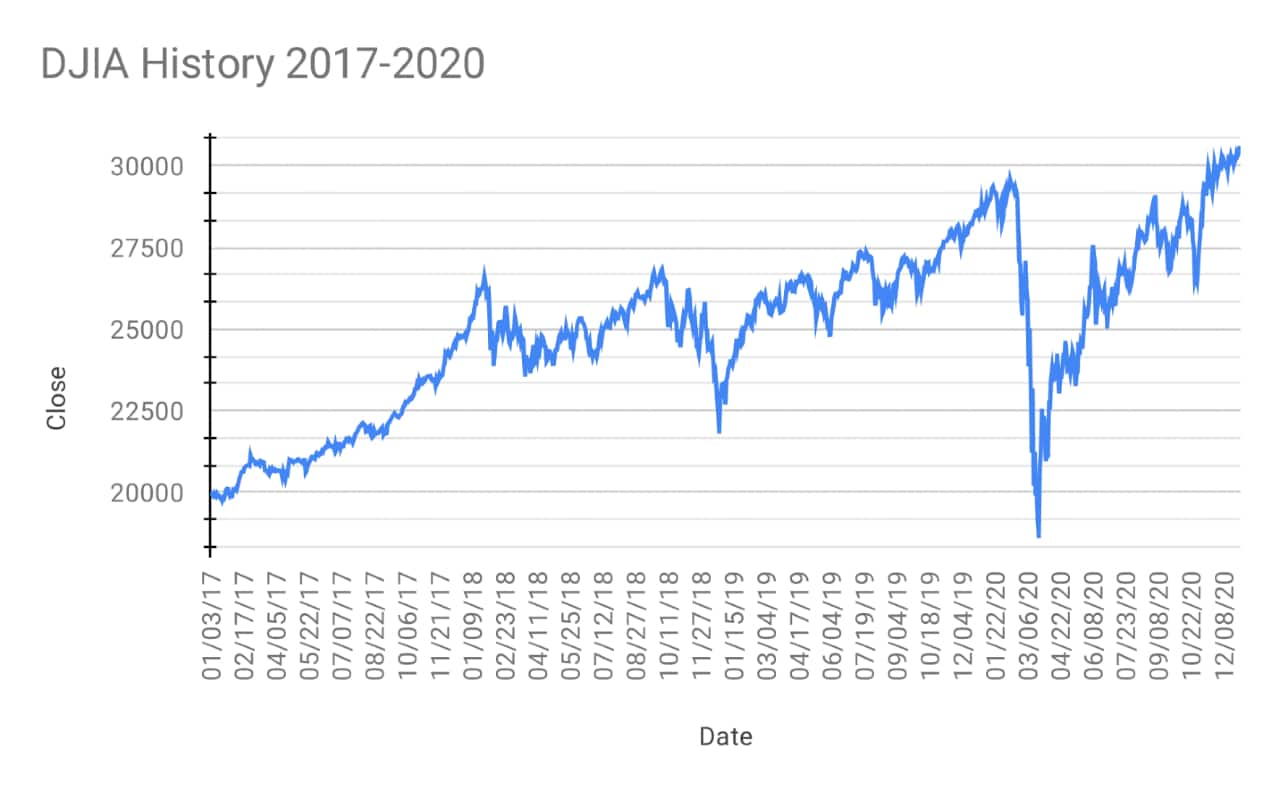
Beyond such patterns, mathematics offers two fundamental but somewhat opposing paradigms for the market. The first is randomness, i.e. changes are unpredictable, due to the unpredictable way news of mergers, losses, environmental events, and other influencing factors pop up. So the past cannot forecast the future.
The second is a chaotic model, which holds that changes in prices can be predicted in the short term if we have complete knowledge of influencing factors. However, there is great built-in sensitivity, so that even a tiny deviation or inaccuracy in data can lead to completely different results down the road (the butterfly effect). The real market probably incorporates both types of behaviour.
The above are some of the (formula-free!) ideas that mathematics provides to help us understand the stock market. But what if we want to actually use them to beat the odds? That’s where the calculation part of maths comes in. This is best left to experts, since financial models can be very complex, and one needs sophisticated techniques to extract even tiny advantages from them. Success is not guaranteed even for the highest paid Wall Street quants.
The way for most investors to practically use mathematics is through forecasting tools. By simulating many different possible scenarios, such tools give you a range of possible returns on your portfolio, each with an associated probability. This enables you to decide what risk you are willing to tolerate in pursuit of your investment goals. Given the complexity of the stock market, that’s the best most of us can do.
